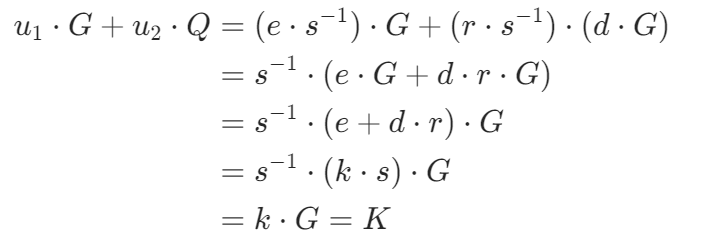ECDSA椭圆曲线数字签名算法

E

ECDSA（Elliptic Curve Digital Signature Algorithm，椭圆曲线数字签名算法）是一种基于椭圆曲线密码学（ECC）的数字签名标准，用于验证数据的完整性（未被篡改）、真实性（确实来自发送方）和不可否认性（发送方无法否认发送行为）

它相比于RSA等签名算法，密钥长度更短，计算效率更高，因而得到广泛应用。

核心流程

ECDSA的核心流程分为密钥生成、签名生成和签名验证三个阶段
需要预先约定一条椭圆曲线E（记其模数为n）、基点 G

1.密钥生成

  • 私钥：随机选择整数 d，满足$ 1<d<n−1$（n 为基点 G 的阶）。
  • 公钥：通过点乘计算$ Q=d⋅G$（Q 是椭圆曲线上的点，与私钥 d 一一对应）。

！！私钥应当严格保密！！

2. 签名生成（发送方操作）

最终生成的签名的形式为(r,s)(r,s)

  1. 计算消息msg的哈希值: h=Hash(msg)h = Hash(msg),取h的整数形式(如果过长，通常阶段至与n同长)
  2. 生成随机整数k，满足1<k<n−11<k<n-1
  3. 计算点K=k⋅GK = k\cdot G,再计算r=K.xmod  nr = K.x \mod{n} (这里使用K.xK.x表示K的x轴坐标，注意要满足r≠0r\not = 0)
  4. 计算k的逆元k−1mod  nk^{-1}\mod{n}
  5. 计算s=(k−1⋅(h+d⋅r))mod  ns=(k^{-1}\cdot(h+d\cdot r))\mod{n} (注意要满足s≠0s\not = 0)
  6. 签名结果为 (r,s)(r,s)，与消息 m 一同发送。

3.签名验证（接收方操作）

接收方收到消息 m 和签名 (r,s)(r,s) 后，验证步骤：

  1. 检查 r 和 s 是否满足 1≤r,s<n1≤r,s<n，若不满足则签名无效。
  2. 计算消息哈希值 h=Hash(m)（与发送方使用相同哈希函数）。
  3. 计算 s 的逆元 s−1mod  ns^{−1}\mod{n}。
  4. 计算 u1=(h⋅s−1)mod  nu_1=(h\cdot s^{−1})\mod{n} 和 u2=(r⋅s−1)mod  nu_2=(r\cdot s^{−1})\mod{n}。
  5. 计算点 P=u1⋅G+u2⋅QP=u_1⋅G+u_2⋅Q（Q 是发送方的公钥）。若 P=O（无穷远点），则签名无效。
  6. 取 P 的 x 坐标 P.xP.x，计算 v=P.xmod  nv=P.x\mod{n}。若 v=r，则签名有效；否则无效。

杂谈，r和s的设计逻辑

根据上面的步骤我们可以发现，签名生成的过程中，可以看作是生成了一个临时的公钥K=k⋅GK = k\cdot G

r是K的x轴坐标，r就只与临时私钥k有关，只要k不同，r就不同，确保了签名的随机性

而s则将私钥、消息、临时私钥相关联，使得任意一个值被篡改都会影响签名验证

之后在签名验证操作中，检验的逻辑核心是看利用s和r能否还原出K=k⋅GK = k\cdot G

计算过程如下

img