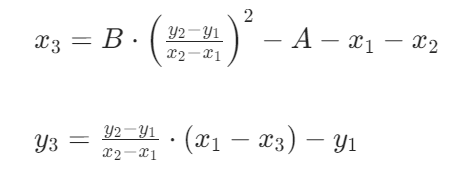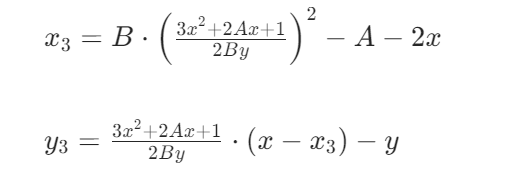蒙哥马利阶梯算法

w

蒙哥马利阶梯算法的核心是通过 “二进制分解 + 固定步骤迭代” 实现对一个 “标量”（整数）的高效计算，经常用于做点标量乘法和模幂运算

本文主要讲解蒙哥马利阶梯算法在ECC上点标量乘法的计算

蒙哥马利阶梯算法（Montgomery Ladder）

蒙哥马利阶梯算法是一种通用的算法，但它与蒙哥马利曲线结合时效率更高

要理解蒙哥马利阶梯算法如何计算点的标量乘法，我们还得把Double and Add算法拉过来打配合

我们知道Double and Add算法的基本流程

假如求5P

我们把5用二进制表示为101

根据二进制各位的权值，遍历每一位的时候都有乘法，但会有一个很重要的if语句：

1
2
if n == 1:
	add_point

而在n == 0的时候显然少了一步点加操作

这就会导致我们的算法在处理0和1时，工作的时长有明显差异

而又有那么一种很不传统的密码分析方法——侧信道攻击，即通过分析时间、功耗、电磁辐射、声音甚至温度变化等物理信息来分析

这就会使得我们的密码不那么安全

而蒙哥马利算法在0和1上的步骤差异很小，能有效避免侧信道攻击

蒙哥马利算法的步骤如下：

1
2
3
4
5
6
1.初始化
设R0=P,R1=[2]P
2.迭代处理从二进制数k的次高位到第0位
	如果当前位为0，R0=[2]R0,R1=R0+R1
	如果当前位为1，R0=R0+R1,R1=[2]R1
3.迭代结束后，R0即为[k]G,返回其x坐标

看上去挺简单的4不4

img

然后我们还需要考虑一个问题，我们前面说蒙哥马利算法在与蒙哥马利曲线搭配时效果最佳

那我们还得介绍蒙哥马利曲线，以及在蒙哥马利曲线上的计算公式

蒙哥马利曲线

蒙哥马利形式的椭圆曲线方程定义为:

By2=x3+Ax2+x,其中A,B∈K(K为一个域)，且B(A2−4)≠0By^2=x^3+Ax^2+x,其中A,B\in K(K为一个域)，且B(A^2-4) \not = 0

例如经常使用的蒙哥马利曲线Curve25519:y2=x3+486662x2+xmod  2255−19y^2=x^3+486662x^2+x \mod{2^{255}−19}

此方程在仿射坐标上的加法公式

img

此方程在仿射坐标上的倍点公式

img

此外，两公式都可以转化为忽略y，仅计算x的形式，分别为：

加：x3=1B⋅((x1x2−1)2(x1−x2)2)−A−x1−x2mod  p倍：x3=(x2−1)24x(x2+Ax+1)mod  p加：x_3 = \frac{1}{B} \cdot (\frac{(x_1x_2-1)^2}{(x_1-x_2)^2})-A-x_1-x_2\mod{p}\\ 倍：x_3 = \frac{(x^2-1)^2}{4x(x^2+Ax+1)}\mod{p}